1203. Sort Items by Groups Respecting Dependencies

Problem Link

Description

---

There are n items each belonging to zero or one of m groups where group[i] is the group that the i-th item belongs to and it's equal to -1 if the i-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.

Return a sorted list of the items such that:

• The items that belong to the same group are next to each other in the sorted list.
• There are some relations between these items where beforeItems[i] is a list containing all the items that should come before the i-th item in the sorted array (to the left of the i-th item).

Return any solution if there is more than one solution and return an empty list if there is no solution.

 

Example 1:

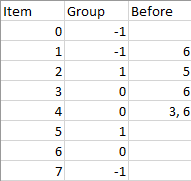
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
Output: [6,3,4,1,5,2,0,7]

Example 2:

Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
Output: []
Explanation: This is the same as example 1 except that 4 needs to be before 6 in the sorted list.

 

Constraints:

• 1 <= m <= n <= 3 * 104
• group.length == beforeItems.length == n
• -1 <= group[i] <= m - 1
• 0 <= beforeItems[i].length <= n - 1
• 0 <= beforeItems[i][j] <= n - 1
• i != beforeItems[i][j]
• beforeItems[i] does not contain duplicates elements.

Solution

---

Python3

def topo_sort(predecessors, successors):
    order = []
    available = [i for i in range(len(predecessors)) if not predecessors[i]]
    while available:
        i = available.pop()
        order.append(i)
        for j in successors[i]:
            predecessors[j] -= 1
            if not predecessors[j]:
                available.append(j)
    return order
 
class Solution:
    def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:
        for i in range(n):
            if group[i] == -1:
                group[i] = m
                m += 1
        
        item_predecessors = [0] * n
        group_predecessors = [0] * m
        item_successors = [[] for _ in range(n)]
        group_successors = [[] for _ in range(m)]
        for i, (group_i, before_i) in enumerate(zip(group, beforeItems)):
            for j in before_i:
                item_predecessors[i] += 1
                item_successors[j].append(i)
                if group_i != group[j]:
                    group_predecessors[group_i] += 1
                    group_successors[group[j]].append(group_i)
        
        item_order = topo_sort(item_predecessors, item_successors)
        group_order = topo_sort(group_predecessors, group_successors)
        if len(item_order) != n or len(group_order) != m:
            return []
        
        group_orders = [[] for _ in range(m)]
        for i in item_order:
            group_orders[group[i]].append(i)
        
        return sum((group_orders[g] for g in group_order), [])