2658. Maximum Number of Fish in a Grid

Problem Link

Description

---

You are given a 0-indexed 2D matrix grid of size m x n, where (r, c) represents:

• A land cell if grid[r][c] = 0, or
• A water cell containing grid[r][c] fish, if grid[r][c] > 0.

A fisher can start at any water cell (r, c) and can do the following operations any number of times:

• Catch all the fish at cell (r, c), or
• Move to any adjacent water cell.

Return the maximum number of fish the fisher can catch if he chooses his starting cell optimally, or 0 if no water cell exists.

An adjacent cell of the cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) or (r - 1, c) if it exists.

 

Example 1:

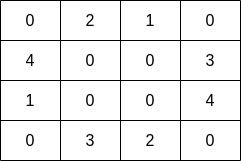
Input: grid = [[0,2,1,0],[4,0,0,3],[1,0,0,4],[0,3,2,0]]
Output: 7
Explanation: The fisher can start at cell (1,3) and collect 3 fish, then move to cell (2,3) and collect 4 fish.

Example 2:

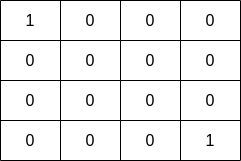
Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,1]]
Output: 1
Explanation: The fisher can start at cells (0,0) or (3,3) and collect a single fish. 

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• 0 <= grid[i][j] <= 10

Solution

---

Python3

class Solution:
    def findMaxFish(self, grid: List[List[int]]) -> int:
        rows, cols = len(grid), len(grid[0])
        res = 0
 
        def go(x, y):
            total = grid[x][y]
            grid[x][y] = 0
 
            for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
                if 0 <= dx < rows and 0 <= dy < cols and grid[dx][dy] != 0:
                    total += go(dx, dy)
 
            return total
        
        for x in range(rows):
            for y in range(cols):
                if grid[x][y] != 0:
                    res = max(res, go(x, y))
 
        return res