2556. Disconnect Path in a Binary Matrix by at Most One Flip

Problem Link

Description

---

You are given a 0-indexed m x n binary matrix grid. You can move from a cell (row, col) to any of the cells (row + 1, col) or (row, col + 1) that has the value 1. The matrix is disconnected if there is no path from (0, 0) to (m - 1, n - 1).

You can flip the value of at most one (possibly none) cell. You cannot flip the cells (0, 0) and (m - 1, n - 1).

Return true if it is possible to make the matrix disconnect or false otherwise.

Note that flipping a cell changes its value from 0 to 1 or from 1 to 0.

 

Example 1:

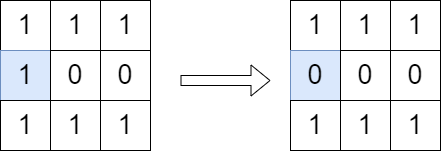
Input: grid = [[1,1,1],[1,0,0],[1,1,1]]
Output: true
Explanation: We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.

Example 2:

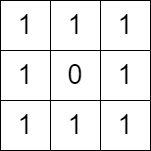
Input: grid = [[1,1,1],[1,0,1],[1,1,1]]
Output: false
Explanation: It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 1000
• 1 <= m * n <= 105
• grid[i][j] is either 0 or 1.
• grid[0][0] == grid[m - 1][n - 1] == 1

Solution

---

Python3

class Solution:
    def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:
        rows, cols = len(grid), len(grid[0])
        
        def dfs(x, y):
            if x + 1 == rows and y + 1 == cols: return True
 
            if x >= rows or y >= cols or grid[x][y] == 0: return False
 
            grid[x][y] = 0
 
            return dfs(x + 1, y) or dfs(x, y + 1)
        
        if not dfs(0, 0): return True
        grid[0][0] = 1
 
        return not dfs(0, 0)

C++

class Solution {
public:
    bool dfs(vector<vector<int>> &grid, int i, int j){ 
        if(i+1 == grid.size() && j+1 == grid[0].size()) return true;
        if(i >= grid.size() || j >= grid[0].size() || grid[i][j] == 0) return false;
        grid[i][j] = 0;
        return dfs(grid, i+1, j) || dfs(grid, i, j+1);
    }
 
    bool isPossibleToCutPath(vector<vector<int>>& grid) { 
        if(dfs(grid, 0, 0) == false) return true;
        grid[0][0] = 1;
        return !dfs(grid, 0, 0);
    }
};