2096. Step-By-Step Directions From a Binary Tree Node to Another

Problem Link

Description

---

You are given the root of a binary tree with n nodes. Each node is uniquely assigned a value from 1 to n. You are also given an integer startValue representing the value of the start node s, and a different integer destValue representing the value of the destination node t.

Find the shortest path starting from node s and ending at node t. Generate step-by-step directions of such path as a string consisting of only the uppercase letters 'L', 'R', and 'U'. Each letter indicates a specific direction:

• 'L' means to go from a node to its left child node.
• 'R' means to go from a node to its right child node.
• 'U' means to go from a node to its parent node.

Return the step-by-step directions of the shortest path from node s to node t.

 

Example 1:

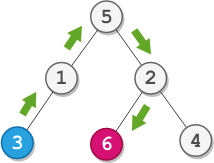
Input: root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6
Output: "UURL"
Explanation: The shortest path is: 3 → 1 → 5 → 2 → 6.

Example 2:

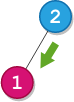
Input: root = [2,1], startValue = 2, destValue = 1
Output: "L"
Explanation: The shortest path is: 2 → 1.

 

Constraints:

• The number of nodes in the tree is n.
• 2 <= n <= 105
• 1 <= Node.val <= n
• All the values in the tree are unique.
• 1 <= startValue, destValue <= n
• startValue != destValue

Solution

---

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* findLCA(TreeNode* node, int start, int end) {
        if (!node) return NULL;
 
        if (node->val == start || node->val == end) return node;
 
        TreeNode* left = findLCA(node->left, start, end);
        TreeNode* right = findLCA(node->right, start, end);
 
        if (left && right) return node;
 
        return left ? left : right;
    }
 
    bool dfs(TreeNode* node, string& path, int val)  {
        if (!node) return false;
 
        if (node->val == val) return true;
 
        path.push_back('L');
        if (dfs(node->left, path, val)) return true;
        path.pop_back();
 
        path.push_back('R');
        if (dfs(node->right, path, val)) return true;
        path.pop_back();
 
        return false;
    }
 
    string getDirections(TreeNode* root, int startValue, int destValue) {
        TreeNode* lca = findLCA(root, startValue, destValue);
        string start = "", end = "";
 
        dfs(lca, start, startValue);
        dfs(lca, end, destValue);
 
        for (auto& c : start) c = 'U';
 
        return start + end;
    }
};

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
 
class Solution:
    def getDirections(self, root: Optional[TreeNode], startValue: int, destValue: int) -> str:
        nodes = collections.defaultdict(tuple)
        
        def go(node, parent):
            if not node: return
            
            nodes[node.val] = (parent, node)
            
            go(node.left, node.val)
            go(node.right, node.val)
        
        go(root, -1)
        
        deq = collections.deque([(startValue, "")])
        visited = set([startValue])
        
        while deq:
            x, path = deq.popleft()
 
            if x == destValue: return path
            
            if x == -1: continue
            parent, node = nodes[x]
            
            if parent not in visited:
                visited.add(parent)
                deq.append((parent, path + "U"))
            
            if node.left and node.left.val not in visited:
                visited.add(node.left.val)
                deq.append((node.left.val, path + "L"))
            
            if node.right and node.right.val not in visited:
                visited.add(node.right.val)
                deq.append((node.right.val, path + "R"))