2440. Create Components With Same Value

Problem Link

Description

---

There is an undirected tree with n nodes labeled from 0 to n - 1.

You are given a 0-indexed integer array nums of length n where nums[i] represents the value of the ith node. You are also given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

You are allowed to delete some edges, splitting the tree into multiple connected components. Let the value of a component be the sum of all nums[i] for which node i is in the component.

Return the maximum number of edges you can delete, such that every connected component in the tree has the same value.

 

Example 1:

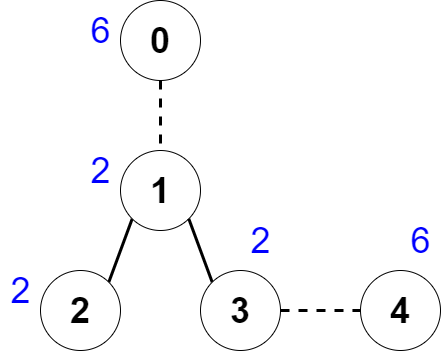
Input: nums = [6,2,2,2,6], edges = [[0,1],[1,2],[1,3],[3,4]] 
Output: 2 
Explanation: The above figure shows how we can delete the edges [0,1] and [3,4]. The created components are nodes [0], [1,2,3] and [4]. The sum of the values in each component equals 6. It can be proven that no better deletion exists, so the answer is 2.

Example 2:

Input: nums = [2], edges = []
Output: 0
Explanation: There are no edges to be deleted.

 

Constraints:

• 1 <= n <= 2 * 104
• nums.length == n
• 1 <= nums[i] <= 50
• edges.length == n - 1
• edges[i].length == 2
• 0 <= edges[i][0], edges[i][1] <= n - 1
• edges represents a valid tree.

Solution

---

Python3

class Solution:
    def componentValue(self, nums: List[int], edges: List[List[int]]) -> int:
        N = len(nums)
        graph = defaultdict(list)
        total = sum(nums)
        
        for a, b in edges:
            graph[a].append(b)
            graph[b].append(a)
        
        def good(divisor):
            if total % divisor != 0: return False
            
            target = total // divisor
            count = 0
            visited = [False] * N
            
            def dfs(node):
                nonlocal count
                
                if visited[node]: return 0    
                visited[node] = True
                
                curr = nums[node]
                
                for nei in graph[node]:
                    curr += dfs(nei)
                
                if curr == target:
                    count += 1
                    curr = 0
                
                return curr
                
            dfs(0)
            return count == divisor
        
        for divisor in range(N, 0, -1):
            if good(divisor):
                return divisor - 1
        
        return 0