1361. Validate Binary Tree Nodes

Problem Link

Description

---

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

 

Example 1:

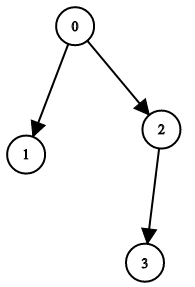
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

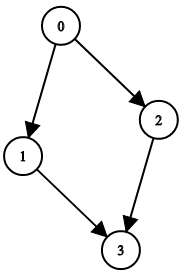
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

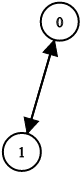
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

 

Constraints:

• n == leftChild.length == rightChild.length
• 1 <= n <= 104
• -1 <= leftChild[i], rightChild[i] <= n - 1

Solution

---

Python3

class Solution:
    def countNodes(self, root, leftChild, rightChild):
        if root == -1:
            return 0
        
        return 1 + self.countNodes(leftChild[root], leftChild, rightChild) + self.countNodes(rightChild[root], leftChild, rightChild)
 
    def validateBinaryTreeNodes(self, n: int, leftChild: List[int], rightChild: List[int]) -> bool:
        indegree = [0] * n
        root = None
 
        for i, (left, right) in enumerate(zip(leftChild, rightChild)):
            if left != -1:
                indegree[left] += 1
 
                if indegree[left] > 1:
                    return False
            
            if right != -1:
                indegree[right] += 1
 
                if indegree[right] > 1:
                    return False
        
        for i in range(n):
            if indegree[i] == 0:
                if root is not None: 
                    return False
 
                root = i
        
        if root is None:
            return False
        
        return self.countNodes(root, leftChild, rightChild) == n

C++

class Solution {
public:
   int countNodes(vector<int> &l,vector<int> &r,int root)   // DFS from root to validate that all nodes are visited.
    {
        if(root==-1)
            return 0;
        return 1+countNodes(l,r,l[root])+countNodes(l,r,r[root]);
    }
    bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) 
    {
        vector<int> inDegree(n,0);
        int root=-1;
        for(int i=0;i<leftChild.size();i++)
            if(leftChild[i]!=-1&&inDegree[leftChild[i]]++==1)  //If in-degree exceeds 1 return false.
                return false;
            else if(rightChild[i]!=-1&&inDegree[rightChild[i]]++==1)  //If in-degree exceeds 1 return false.
                return false;
        for(int i=0;i<leftChild.size();i++)    //Find root and also check for multiple roots.
            if(inDegree[i]==0)  //If in-degree = 0 and has children it's a root.
                if(root==-1)   //Store the root.
                    root=i;
                else    //We have multiple roots, return false
                    return false;
        if(root==-1)
            return false;
        return countNodes(leftChild,rightChild,root)==n;
    }
};