1697. Checking Existence of Edge Length Limited Paths

Problem Link

Description

---

An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [ui, vi, disi] denotes an edge between nodes ui and vi with distance disi. Note that there may be multiple edges between two nodes.

Given an array queries, where queries[j] = [pj, qj, limitj], your task is to determine for each queries[j] whether there is a path between pj and qj such that each edge on the path has a distance strictly less than limitj .

Return a boolean array answer, where answer.length == queries.length and the jth value of answer is true if there is a path for queries[j] is true, and false otherwise.

 

Example 1:

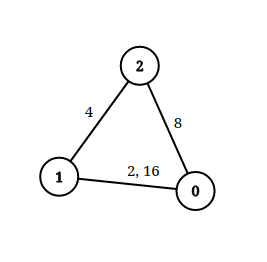
Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
Output: [false,true]
Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.

Example 2:

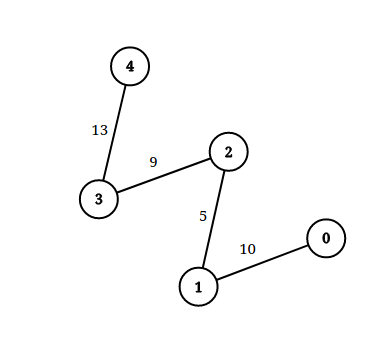
Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
Output: [true,false]
Explanation: The above figure shows the given graph.

 

Constraints:

• 2 <= n <= 105
• 1 <= edgeList.length, queries.length <= 105
• edgeList[i].length == 3
• queries[j].length == 3
• 0 <= ui, vi, pj, qj <= n - 1
• ui != vi
• pj != qj
• 1 <= disi, limitj <= 109
• There may be multiple edges between two nodes.

Solution

---

Python3

class UnionFind:
    def __init__(self, N):
        self._parent = list(range(N))
        self._size = [1] * N
    def union(self, a, b):
        a, b = self.find(a), self.find(b)
        if a == b:
            return
        if self._size[a] < self._size[b]:
            a, b = b, a
        self._parent[b] = a
        self._size[a] += self._size[b]
 
    def find(self, x):
        while self._parent[x] != x:
            self._parent[x] = self._parent[self._parent[x]]
            x = self._parent[x]
        return x
 
 
class Solution:
    def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:
        uf = UnionFind(n)
        Q = sorted([(limit, p, q, index) for index, (p, q, limit) in enumerate(queries)])
        edgeList.sort(key = lambda x : x[2])
        res = [False] * len(queries)
        index = 0
 
        for limit, p, q, i in Q:
            while index < len(edgeList) and edgeList[index][2] < limit:
                uf.union(edgeList[index][0], edgeList[index][1])
                index += 1
            
            res[i] = uf.find(p) == uf.find(q)
 
        return res