2493. Divide Nodes Into the Maximum Number of Groups

Problem Link

Description

---

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [ai, bi] indicates that there is a bidirectional edge between nodes ai and bi. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

• Each node in the graph belongs to exactly one group.
• For every pair of nodes in the graph that are connected by an edge [ai, bi], if ai belongs to the group with index x, and bi belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

 

Example 1:

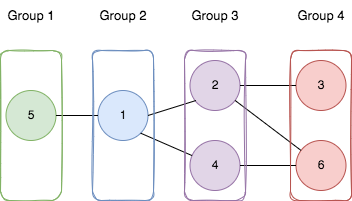
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
Output: 4
Explanation: As shown in the image we:
- Add node 5 to the first group.
- Add node 1 to the second group.
- Add nodes 2 and 4 to the third group.
- Add nodes 3 and 6 to the fourth group.
We can see that every edge is satisfied.
It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

Input: n = 3, edges = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied.
It can be shown that no grouping is possible.

 

Constraints:

• 1 <= n <= 500
• 1 <= edges.length <= 104
• edges[i].length == 2
• 1 <= ai, bi <= n
• ai != bi
• There is at most one edge between any pair of vertices.

Solution

---

Python3

def is_bipartite(graph, n):
    color = defaultdict(int)
 
    def go(x):
        for node in graph[x]:
            if node not in color:
                color[node] = -color[x]
                if not go(node):
                    return False
            else:
                if color[x] == color[node]:
                    return False
 
        return True
 
    for i in range(n):
        if i not in color:
            color[i] = 1
            if not go(i):
                return False
 
    return True
                
 
class Solution:
    def magnificentSets(self, N: int, edges: List[List[int]]) -> int:
        graph = defaultdict(list)
        
        for a, b in edges:
            a -= 1
            b -= 1
            graph[a].append(b)
            graph[b].append(a)
        
        if not is_bipartite(graph, N): return -1
        
        groups = []
        grouped = set()
        
        for node in range(N):
            if node in grouped: continue
            
            group = set([node])
            stack = [node]
            
            while stack:
                curr = stack.pop()
                
                for nei in graph[curr]:
                    if nei in group: continue
                    group.add(nei)
                    stack.append(nei)
            
            groups.append(group)
            grouped |= group
        
        res = 0
        for group in groups:
            maxDepth = 0
            
            for start in group:
                depth = {}
                depth[start] = 0
                queue = deque([start])
                
                while queue:
                    node = queue.popleft()
                    
                    for nei in graph[node]:
                        if nei in depth: continue
                        
                        depth[nei] = depth[node] + 1
                        queue.append(nei)
                
                maxDepth = max(maxDepth, max(depth.values()))
                
            res += maxDepth + 1
        
        return res