3161. Block Placement Queries

Problem Link

Description

---

There exists an infinite number line, with its origin at 0 and extending towards the positive x-axis.

You are given a 2D array queries, which contains two types of queries:

1. For a query of type 1, queries[i] = [1, x]. Build an obstacle at distance x from the origin. It is guaranteed that there is no obstacle at distance x when the query is asked.
2. For a query of type 2, queries[i] = [2, x, sz]. Check if it is possible to place a block of size sz anywhere in the range [0, x] on the line, such that the block entirely lies in the range [0, x]. A block cannot be placed if it intersects with any obstacle, but it may touch it. Note that you do not actually place the block. Queries are separate.

Return a boolean array results, where results[i] is true if you can place the block specified in the ith query of type 2, and false otherwise.

 

Example 1:

Input: queries = [[1,2],[2,3,3],[2,3,1],[2,2,2]]

Output: [false,true,true]

Explanation:

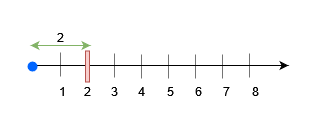
For query 0, place an obstacle at x = 2. A block of size at most 2 can be placed before x = 3.

Example 2:

Input: queries = [[1,7],[2,7,6],[1,2],[2,7,5],[2,7,6]]

Output: [true,true,false]

Explanation:

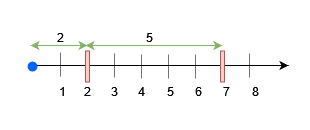
• Place an obstacle at x = 7 for query 0. A block of size at most 7 can be placed before x = 7.
• Place an obstacle at x = 2 for query 2. Now, a block of size at most 5 can be placed before x = 7, and a block of size at most 2 before x = 2.

 

Constraints:

• 1 <= queries.length <= 15 * 104
• 2 <= queries[i].length <= 3
• 1 <= queries[i][0] <= 2
• 1 <= x, sz <= min(5 * 104, 3 * queries.length)
• The input is generated such that for queries of type 1, no obstacle exists at distance x when the query is asked.
• The input is generated such that there is at least one query of type 2.

Solution

---

C++

class Solution {
public:
    int N = 50005;
    int MAX = 4 * 50005 + 5;
    int arr[50005];
    int tree[4 * 50005 + 5];
    int lazy[4 * 50005 + 5];
    int INF = 1e9;
 
    void build(int a[], int v, int tl, int tr) {
        if (tl == tr) {
            tree[v] = a[tl];
        } else {
            int tm = (tl + tr) / 2;
            build(a, v*2, tl, tm);
            build(a, v*2+1, tm+1, tr);
            tree[v] = max(tree[v*2], tree[v*2 + 1]);
        }
    }
 
    void push(int v) {
        tree[v*2] += lazy[v];
        lazy[v*2] += lazy[v];
        tree[v*2+1] += lazy[v];
        lazy[v*2+1] += lazy[v];
        lazy[v] = 0;
    }
 
    void update(int v, int tl, int tr, int l, int r, int addend) {
        if (l > r) 
            return;
        if (l == tl && tr == r) {
            tree[v] += addend;
            lazy[v] += addend;
        } else {
            push(v);
            int tm = (tl + tr) / 2;
            update(v*2, tl, tm, l, min(r, tm), addend);
            update(v*2+1, tm+1, tr, max(l, tm+1), r, addend);
            tree[v] = max(tree[v*2], tree[v*2+1]);
        }
    }
 
    int query(int v, int tl, int tr, int l, int r) {
        if (l > r)
            return -INF;
        if (l == tl && tr == r)
            return tree[v];
        push(v);
        int tm = (tl + tr) / 2;
        return max(query(v*2, tl, tm, l, min(r, tm)), 
                query(v*2+1, tm+1, tr, max(l, tm+1), r));
    }
 
    vector<bool> getResults(vector<vector<int>>& queries) {
        for(int i=0; i<N; i++) arr[i] = i;
        vector<bool> ans;
        build(arr, 1, 0, N - 1);
        memset(lazy, 0, sizeof lazy);
        set<int> st;
        st.insert(N - 1);
 
        for (auto &it: queries) {
            if (it[0] == 1) {
                int x = it[1];
                int val = query(1, 0, N - 1, x, x);
                int right = *st.lower_bound(x);
                update(1, 0, N - 1, x + 1, right, -1 * val);
                st.insert(x);
            } else {
                int x = it[1], sz = it[2];
                int val = query(1, 0, N - 1, 0, x);
                ans.push_back(val >= sz);
            }
        }
 
        return ans;
    }
};