2661. First Completely Painted Row or Column

Problem Link

Description

---

You are given a 0-indexed integer array arr, and an m x n integer matrix mat. arr and mat both contain all the integers in the range [1, m * n].

Go through each index i in arr starting from index 0 and paint the cell in mat containing the integer arr[i].

Return the smallest index i at which either a row or a column will be completely painted in mat.

 

Example 1:

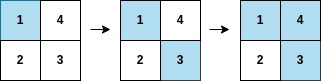
Input: arr = [1,3,4,2], mat = [[1,4],[2,3]]
Output: 2
Explanation: The moves are shown in order, and both the first row and second column of the matrix become fully painted at arr[2].

Example 2:

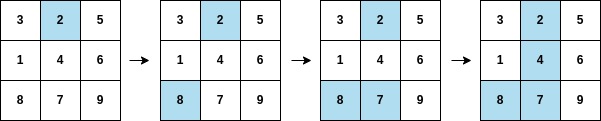
Input: arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]]
Output: 3
Explanation: The second column becomes fully painted at arr[3].

 

Constraints:

• m == mat.length
• n = mat[i].length
• arr.length == m * n
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 1 <= arr[i], mat[r][c] <= m * n
• All the integers of arr are unique.
• All the integers of mat are unique.

Solution

---

Python3

class Solution:
    def firstCompleteIndex(self, arr: List[int], mat: List[List[int]]) -> int:
        rows, cols = len(mat), len(mat[0])
        R, C = {}, {}
 
        for i in range(rows):
            for j in range(cols):
                R[mat[i][j]] = i
                C[mat[i][j]] = j
        
        currRow, currCol = [0] * rows , [0] * cols
        for i, x in enumerate(arr):
            currRow[R[x]] += 1
            currCol[C[x]] += 1
 
            if currRow[R[x]] == cols or currCol[C[x]] == rows:
                return i
        
        return -1