606. Construct String from Binary Tree

Problem Link

Description

---

Given the root node of a binary tree, your task is to create a string representation of the tree following a specific set of formatting rules. The representation should be based on a preorder traversal of the binary tree and must adhere to the following guidelines:

• Node Representation: Each node in the tree should be represented by its integer value.

• Parentheses for Children: If a node has at least one child (either left or right), its children should be represented inside parentheses. Specifically:

  <ul>
  	<li>If a node has a left child, the value of the left child should be enclosed in parentheses immediately following the node&#39;s value.</li>
  	<li>If a node has a right child, the value of the right child should also be enclosed in parentheses. The parentheses for the right child should follow those of the left child.</li>
  </ul>
  </li>
  <li>
  <p><strong>Omitting Empty Parentheses</strong>: Any empty parentheses pairs (i.e., <code>()</code>) should be omitted from the final string representation of the tree, with one specific exception: when a node has a right child but no left child. In such cases, you must include an empty pair of parentheses to indicate the absence of the left child. This ensures that the one-to-one mapping between the string representation and the original binary tree structure is maintained.</p>
  
  <p>In summary, empty parentheses pairs should be omitted when a node has only a left child or no children. However, when a node has a right child but no left child, an empty pair of parentheses must precede the representation of the right child to reflect the tree&#39;s structure accurately.</p>
  </li>
  

 

Example 1:

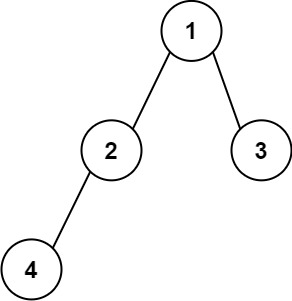
Input: root = [1,2,3,4]
Output: "1(2(4))(3)"
Explanation: Originally, it needs to be "1(2(4)())(3()())", but you need to omit all the empty parenthesis pairs. And it will be "1(2(4))(3)".

Example 2:

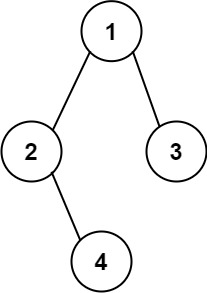
Input: root = [1,2,3,null,4]
Output: "1(2()(4))(3)"
Explanation: Almost the same as the first example, except the () after 2 is necessary to indicate the absence of a left child for 2 and the presence of a right child.

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -1000 <= Node.val <= 1000

Solution

---

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def tree2str(self, root: Optional[TreeNode]) -> str:
        
        def go(node):
            if not node: return ""
 
            res = str(node.val)
 
            left, right = go(node.left), go(node.right)
 
            if left or right:
                res += "(" + left + ")"
            
            if right:
                res += "(" + right + ")"
            
            return res
        
        return go(root)