2392. Build a Matrix With Conditions

Problem Link

Description

---

You are given a positive integer k. You are also given:

• a 2D integer array rowConditions of size n where rowConditions[i] = [abovei, belowi], and
• a 2D integer array colConditions of size m where colConditions[i] = [lefti, righti].

The two arrays contain integers from 1 to k.

You have to build a k x k matrix that contains each of the numbers from 1 to k exactly once. The remaining cells should have the value 0.

The matrix should also satisfy the following conditions:

• The number abovei should appear in a row that is strictly above the row at which the number belowi appears for all i from 0 to n - 1.
• The number lefti should appear in a column that is strictly left of the column at which the number righti appears for all i from 0 to m - 1.

Return any matrix that satisfies the conditions. If no answer exists, return an empty matrix.

 

Example 1:

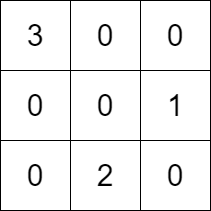
Input: k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]]
Output: [[3,0,0],[0,0,1],[0,2,0]]
Explanation: The diagram above shows a valid example of a matrix that satisfies all the conditions.
The row conditions are the following:
- Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix.
- Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix.
The column conditions are the following:
- Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix.
- Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix.
Note that there may be multiple correct answers.

Example 2:

Input: k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]]
Output: []
Explanation: From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.
No matrix can satisfy all the conditions, so we return the empty matrix.

 

Constraints:

• 2 <= k <= 400
• 1 <= rowConditions.length, colConditions.length <= 104
• rowConditions[i].length == colConditions[i].length == 2
• 1 <= abovei, belowi, lefti, righti <= k
• abovei != belowi
• lefti != righti

Solution

---

C++

class Solution {
public:
    // With Kahn's algorithm
    vector<int> topoSort(vector<vector<int>>& A, int k) {
        vector<int> indegree(k);
        vector<vector<int>> graph(k);
        queue<int> q;
 
        for (auto& condition : A) {
            int u = condition[0] - 1, v = condition[1] - 1;
            graph[u].push_back(v);
            indegree[v]++;
        }
 
        for (int i = 0; i < k; i++) {
            if (indegree[i] == 0) q.push(i);
        }
 
        vector<int> order;
 
        while (!q.empty()) {
            int node = q.front(); q.pop();
            order.push_back(node);
 
            for (int adj: graph[node]) {
                indegree[adj]--;
                if (indegree[adj] == 0) {
                    q.push(adj);
                }
            }
        }
 
        if (order.size() != k) return vector<int>();
 
        return order;
    }
 
    vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {
        int rows = rowConditions.size(), cols = colConditions.size();
        vector<int> topoRow = topoSort(rowConditions, k), topoCol = topoSort(colConditions, k);
 
        if (topoRow.empty() || topoCol.empty()) return vector<vector<int>>();
 
        vector<vector<int>> ans(k, vector<int>(k));
        vector<int> rowMp(k), colMp(k);
 
        for (int i = 0; i < k; i++) {
            rowMp[topoRow[i]] = i;
            colMp[topoCol[i]] = i;
        }
 
        for (int i = 0; i < k; i++) {
            ans[rowMp[i]][colMp[i]] = i + 1;
        }
 
        return ans;
 
    }
};

Python3

class Solution:
    def buildMatrix(self, k: int, rowConditions: List[List[int]], colConditions: List[List[int]]) -> List[List[int]]:
        res = [[0] * k for _ in range(k)]
        
        def topoSort(A):
            adj = [[] for _ in range(k + 1)] 
            
            for a, b in A:
                adj[a].append(b)
            
            seen = [False] * (k + 1)
            order = []
            
            def dfs(x):
                if seen[x]: return
                
                seen[x] = True
                
                for nei in adj[x]:
                    if not seen[nei]:
                        dfs(nei)
                
                order.append(x)
            
            for x in range(1, k + 1):
                dfs(x)
            
            order.reverse()
            M = {j: i for i, j in enumerate(order)}
            
            if all(M[i] < M[j] for i, j in A):
                return order
            
            return None
        
        R = topoSort(rowConditions)
        C = topoSort(colConditions)
        
        if R is None or C is None:
            return []
        
        RM = {j : i for i, j in enumerate(R)}
        CM = {j : i for i, j in enumerate(C)}
        
        for x in range(1, k + 1):
            res[RM[x]][CM[x]] = x
            
        return res