840. Magic Squares In Grid

Problem Link

Description

---

A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.

Given a row x col grid of integers, how many 3 x 3 magic square subgrids are there?

Note: while a magic square can only contain numbers from 1 to 9, grid may contain numbers up to 15.

 

Example 1:

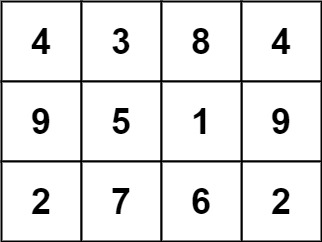
Input: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]]
Output: 1
Explanation: 
The following subgrid is a 3 x 3 magic square:

while this one is not:

In total, there is only one magic square inside the given grid.

Example 2:

Input: grid = [[8]]
Output: 0

 

Constraints:

• row == grid.length
• col == grid[i].length
• 1 <= row, col <= 10
• 0 <= grid[i][j] <= 15

Solution

---

Python3

class Solution:
    def numMagicSquaresInside(self, grid: List[List[int]]) -> int:
        cnt = 0
        # Construct the 3x3 square
        for i in range(len(grid)-2):
            for j in range(len(grid)-2):
                temp_grid = [grid[i+k][j:j+3] for k in range(3)]
                if self.isMagicSquare(temp_grid):
                    cnt += 1
        
        return cnt
        
    
    def isMagicSquare(self, grid):
        '''
        Check whether the given grid is a magic square
        '''
        # Check the elements
        flat = [num for row in grid for num in row]
        if sorted(flat) != [1, 2, 3, 4, 5, 6, 7, 8, 9]:
            return False
        
        # Check the row, column and diagnal sums
        row_sums = [sum(row) for row in grid]
        col_sums = [sum([row[i] for row in grid]) for i in range(3)]
        diag_sums = [sum([grid[i][i] for i in range(3)]), (grid[0][2] + grid[1][1] + grid[2][0])]
        row_sums.extend(col_sums)
        row_sums.extend(diag_sums)
        return len(set(row_sums)) == 1