Description
You are given a m x n 2D array board representing a chessboard, where board[i][j] represents the value of the cell (i, j).
Rooks in the same row or column attack each other. You need to place three rooks on the chessboard such that the rooks do not attack each other.
Return the maximum sum of the cell values on which the rooks are placed.
Example 1:
Input: board = [[-3,1,1,1],[-3,1,-3,1],[-3,2,1,1]]
Output: 4
Explanation:
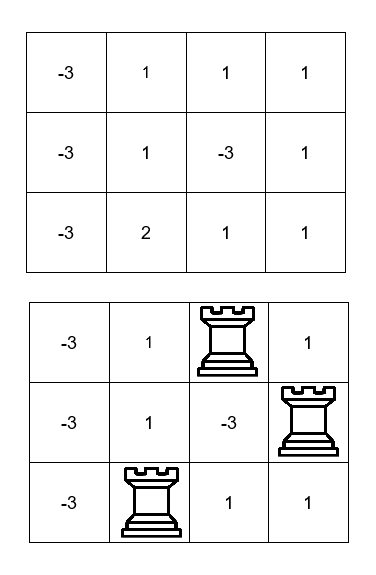
We can place the rooks in the cells (0, 2), (1, 3), and (2, 1) for a sum of 1 + 1 + 2 = 4.
Example 2:
Input: board = [[1,2,3],[4,5,6],[7,8,9]]
Output: 15
Explanation:
We can place the rooks in the cells (0, 0), (1, 1), and (2, 2) for a sum of 1 + 5 + 9 = 15.
Example 3:
Input: board = [[1,1,1],[1,1,1],[1,1,1]]
Output: 3
Explanation:
We can place the rooks in the cells (0, 2), (1, 1), and (2, 0) for a sum of 1 + 1 + 1 = 3.
Constraints:
3 <= m == board.length <= 5003 <= n == board[i].length <= 500-109 <= board[i][j] <= 109
Solution
Python3
class Solution:
def maximumValueSum(self, board: List[List[int]]) -> int:
rows, cols = len(board), len(board[0])
top3 = [nlargest(3, [(board[r][c], c) for c in range(cols)]) for r in range(rows)]
def process(A):
ans = [] # ans[r] = top3 choices for A[..r]
best = []
for row in A:
best.extend(row)
best.sort(reverse = True)
nbest = []
for v, c in best:
if all(c != c0 for v0, c0 in nbest):
nbest.append((v, c))
if len(nbest) == 3: break
ans.append(nbest[:3][:])
return ans
prefix = process(top3)
suffix = process(top3[::-1])[::-1]
res = -inf
for r in range(1, rows - 1):
for v1, c1 in prefix[r - 1]:
for v2, c2 in top3[r]:
for v3, c3 in suffix[r + 1]:
if c1 != c2 and c1 != c3 and c2 != c3:
res = max(res, v1 + v2 + v3)
return res