1914. Cyclically Rotating a Grid

Problem Link

Description

---

You are given an m x n integer matrix grid​​​, where m and n are both even integers, and an integer k.

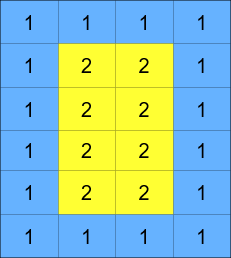
The matrix is composed of several layers, which is shown in the below image, where each color is its own layer:

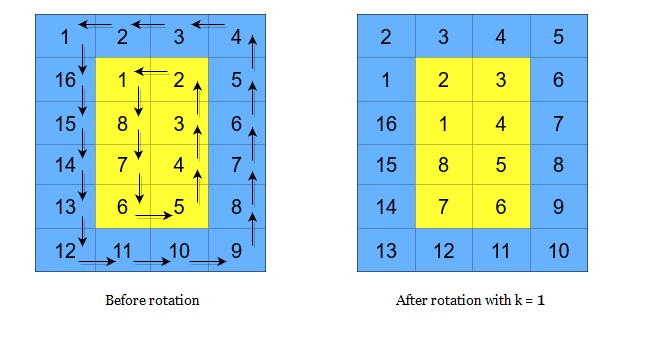
A cyclic rotation of the matrix is done by cyclically rotating each layer in the matrix. To cyclically rotate a layer once, each element in the layer will take the place of the adjacent element in the counter-clockwise direction. An example rotation is shown below:

Return the matrix after applying k cyclic rotations to it.

 

Example 1:

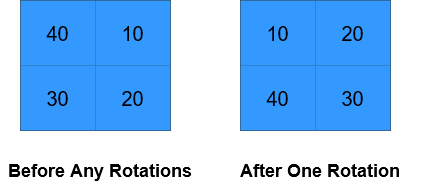
Input: grid = [[40,10],[30,20]], k = 1
Output: [[10,20],[40,30]]
Explanation: The figures above represent the grid at every state.

Example 2:

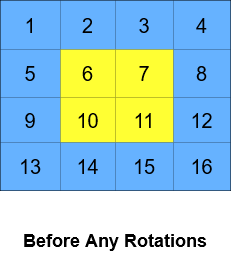
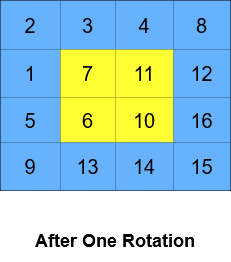
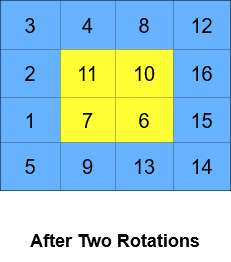
Input: grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2
Output: [[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]]
Explanation: The figures above represent the grid at every state.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 50
• Both m and n are even integers.
• 1 <= grid[i][j] <= 5000
• 1 <= k <= 109

Solution

---

Python3

class Solution:
    def rotateGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
        rows, cols = len(grid), len(grid[0])
        
        for r in range(min(rows, cols) // 2):
            i = j = r
            vals = []
            
            for jj in range(j, cols - j - 1):
                vals.append(grid[i][jj])
            
            for ii in range(i, rows - i - 1):
                vals.append(grid[ii][cols - j - 1])
            
            for jj in range(cols - j - 1, j, -1):
                vals.append(grid[rows - i - 1][jj])
            
            for ii in range(rows - i - 1, i, -1):
                vals.append(grid[ii][j])
            
            kk = k % len(vals)
            vals = vals[kk:] + vals[:kk]
            x = 0
            
            for jj in range(j, cols - j - 1):
                grid[i][jj] = vals[x]; x += 1
            
            for ii in range(i, rows - i - 1):
                grid[ii][cols - j - 1] = vals[x]; x += 1
            
            for jj in range(cols - j - 1, j, -1):
                grid[rows - i - 1][jj] = vals[x]; x += 1
            
            for ii in range(rows - i - 1, i, -1):
                grid[ii][j] = vals[x]; x += 1
        
        return grid