1878. Get Biggest Three Rhombus Sums in a Grid

Problem Link

Description

---

You are given an m x n integer matrix grid​​​.

A rhombus sum is the sum of the elements that form the border of a regular rhombus shape in grid​​​. The rhombus must have the shape of a square rotated 45 degrees with each of the corners centered in a grid cell. Below is an image of four valid rhombus shapes with the corresponding colored cells that should be included in each rhombus sum:

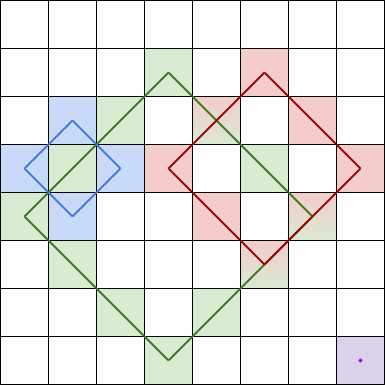
Note that the rhombus can have an area of 0, which is depicted by the purple rhombus in the bottom right corner.

Return the biggest three distinct rhombus sums in the grid in descending order. If there are less than three distinct values, return all of them.

 

Example 1:

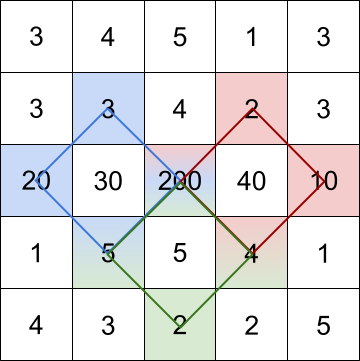
Input: grid = [[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]]
Output: [228,216,211]
Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 20 + 3 + 200 + 5 = 228
- Red: 200 + 2 + 10 + 4 = 216
- Green: 5 + 200 + 4 + 2 = 211

Example 2:

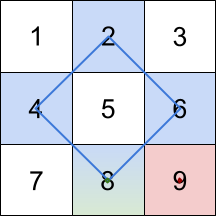
Input: grid = [[1,2,3],[4,5,6],[7,8,9]]
Output: [20,9,8]
Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 4 + 2 + 6 + 8 = 20
- Red: 9 (area 0 rhombus in the bottom right corner)
- Green: 8 (area 0 rhombus in the bottom middle)

Example 3:

Input: grid = [[7,7,7]]
Output: [7]
Explanation: All three possible rhombus sums are the same, so return [7].

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• 1 <= grid[i][j] <= 105

Solution

---

Python3

class Solution:
    def getBiggestThree(self, grid: List[List[int]]) -> List[int]:
        rows, cols = len(grid), len(grid[0])
        res = set()
        
        def isValid(pos):
            return 0 <= pos[0] < rows and 0 <= pos[1] < cols
        
        def calculateTotal(lst, size):
            top, left, right, bottom = lst
            x, y = top
            total = grid[top[0]][top[1]] + grid[bottom[0]][bottom[1]] if size > 0 else grid[top[0]][top[1]]
            
            for i in range(1, size + 1):
                l = (x + i, y - i)
                r = (x + i, y + i)
                total += (grid[l[0]][l[1]] + grid[r[0]][r[1]])
            
            if size > 1:
                x, y = bottom
                for i in range(1, size):
                    l = (x - i, y + i)
                    r = (x - i, y - i)
                    total += (grid[l[0]][l[1]] + grid[r[0]][r[1]])
            
            return total
        
        def dfs(x, y, size):
            top = (x, y)
            left = (x + size, y - size)
            right = (x + size, y + size)
            bottom = (x + (size * 2) , y) if size != 0 else top
            
            lst = [top, left, right, bottom]
            
            if all(isValid(pos) for pos in lst):
                total = calculateTotal(lst, size)
                res.add(total)
                dfs(x, y, size + 1)
        
        for i in range(rows):
            for j in range(cols):
                dfs(i, j, 0)
        
        return sorted(list(res))[::-1][:3]