2876. Count Visited Nodes in a Directed Graph

Problem Link

Description

---

There is a directed graph consisting of n nodes numbered from 0 to n - 1 and n directed edges.

You are given a 0-indexed array edges where edges[i] indicates that there is an edge from node i to node edges[i].

Consider the following process on the graph:

• You start from a node x and keep visiting other nodes through edges until you reach a node that you have already visited before on this same process.

Return an array answer where answer[i] is the number of different nodes that you will visit if you perform the process starting from node i.

 

Example 1:

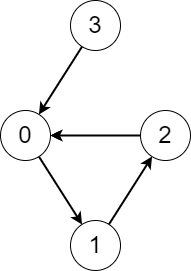
Input: edges = [1,2,0,0]
Output: [3,3,3,4]
Explanation: We perform the process starting from each node in the following way:
- Starting from node 0, we visit the nodes 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 3.
- Starting from node 1, we visit the nodes 1 -> 2 -> 0 -> 1. The number of different nodes we visit is 3.
- Starting from node 2, we visit the nodes 2 -> 0 -> 1 -> 2. The number of different nodes we visit is 3.
- Starting from node 3, we visit the nodes 3 -> 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 4.

Example 2:

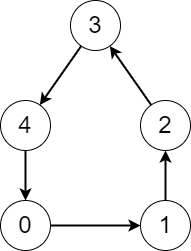
Input: edges = [1,2,3,4,0]
Output: [5,5,5,5,5]
Explanation: Starting from any node we can visit every node in the graph in the process.

 

Constraints:

• n == edges.length
• 2 <= n <= 105
• 0 <= edges[i] <= n - 1
• edges[i] != i

Solution

---

Python3

class Solution:
    def countVisitedNodes(self, edges: List[int]) -> List[int]:
        N = len(edges)
 
        # Kosaraju's Algorithm to find Strongly Connected Components (SCC)
 
        # First DFS on the graph to generate toposort
        visited = [False] * N
        topo = []
 
        def dfs(node):
            if visited[node]: return
 
            visited[node] = True
 
            dfs(edges[node])
 
            topo.append(node)
        
        for node in range(N):
            dfs(node)
 
        # reverse the graph
        transpose = defaultdict(list)
 
        for node, adj in enumerate(edges):
            transpose[adj].append(node)
        
        # Second DFS on the reversed graph to find the cycles
        visited = [False] * N
        comp = 0
        scc = [-1] * N
        sccList = [[] for _ in range(N)]
 
        def dfs2(node):
            if visited[node]: return 
 
            visited[node] = True
            scc[node] = comp
            sccList[comp].append(node)
 
            for adj in transpose[node]:
                dfs2(adj)
        
        while topo:
            node = topo.pop()
 
            if not visited[node]:
                dfs2(node)
                comp += 1
        
        sccCount = [0] * N
        
        for count in range(comp - 1, -1, -1):
            sccCount[count] = len(sccList[count])
            
            for node in sccList[count]:
                adj = edges[node]
 
                if scc[adj] != count:
                    sccCount[count] += sccCount[scc[adj]]
    
        return [sccCount[scc[node]] for node in range(N)]