773. Sliding Puzzle

Problem Link

Description

---

On an 2 x 3 board, there are five tiles labeled from 1 to 5, and an empty square represented by 0. A move consists of choosing 0 and a 4-directionally adjacent number and swapping it.

The state of the board is solved if and only if the board is [[1,2,3],[4,5,0]].

Given the puzzle board board, return the least number of moves required so that the state of the board is solved. If it is impossible for the state of the board to be solved, return -1.

 

Example 1:

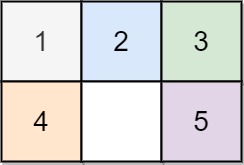
Input: board = [[1,2,3],[4,0,5]]
Output: 1
Explanation: Swap the 0 and the 5 in one move.

Example 2:

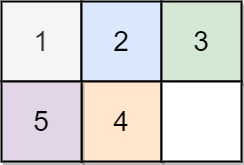
Input: board = [[1,2,3],[5,4,0]]
Output: -1
Explanation: No number of moves will make the board solved.

Example 3:

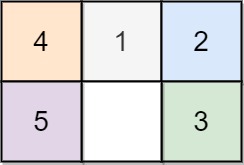
Input: board = [[4,1,2],[5,0,3]]
Output: 5
Explanation: 5 is the smallest number of moves that solves the board.
An example path:
After move 0: [[4,1,2],[5,0,3]]
After move 1: [[4,1,2],[0,5,3]]
After move 2: [[0,1,2],[4,5,3]]
After move 3: [[1,0,2],[4,5,3]]
After move 4: [[1,2,0],[4,5,3]]
After move 5: [[1,2,3],[4,5,0]]

 

Constraints:

• board.length == 2
• board[i].length == 3
• 0 <= board[i][j] <= 5
• Each value board[i][j] is unique.

Solution

---

Python3

class Solution:
    def slidingPuzzle(self, board: List[List[int]]) -> int:
        
        def bt(i0: int, j0: int, step: int) -> None:
            state = tuple(board[0] + board[1])
            if state == target:
                state2min[state] = min(state2min[state], step)
                return
            if state2min[state] <= step: # before / equivalent ans is found
                return
            state2min[state] = step
 
            for ii, jj in [[0,1], [0,-1], [1,0], [-1,0]]:
                ti, tj = i0 + ii, j0 + jj
                if 0 <= ti < 2 and 0 <= tj < 3:
                    board[i0][j0], board[ti][tj] = board[ti][tj], board[i0][j0]
                    bt(ti, tj, step + 1)
                    board[i0][j0], board[ti][tj] = board[ti][tj], board[i0][j0]
 
        
        state2min = defaultdict(lambda: float('inf'))
        target = tuple([1,2,3,4,5,0])
        i0 = j0 = -1
        for i in range(2):
            for j in range(3):
                if board[i][j] == 0:
                    i0, j0 = i, j
        bt(i0, j0, 0)
        return -1 if target not in state2min else state2min[target]