1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree

Problem Link

Description

---

Given a weighted undirected connected graph with n vertices numbered from 0 to n - 1, and an array edges where edges[i] = [ai, bi, weighti] represents a bidirectional and weighted edge between nodes ai and bi. A minimum spanning tree (MST) is a subset of the graph's edges that connects all vertices without cycles and with the minimum possible total edge weight.

Find all the critical and pseudo-critical edges in the given graph's minimum spanning tree (MST). An MST edge whose deletion from the graph would cause the MST weight to increase is called a critical edge. On the other hand, a pseudo-critical edge is that which can appear in some MSTs but not all.

Note that you can return the indices of the edges in any order.

 

Example 1:

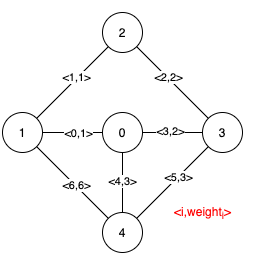
Input: n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
Output: [[0,1],[2,3,4,5]]
Explanation: The figure above describes the graph.
The following figure shows all the possible MSTs:

Notice that the two edges 0 and 1 appear in all MSTs, therefore they are critical edges, so we return them in the first list of the output.
The edges 2, 3, 4, and 5 are only part of some MSTs, therefore they are considered pseudo-critical edges. We add them to the second list of the output.

Example 2:

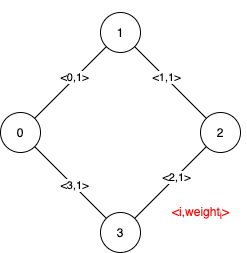
Input: n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
Output: [[],[0,1,2,3]]
Explanation: We can observe that since all 4 edges have equal weight, choosing any 3 edges from the given 4 will yield an MST. Therefore all 4 edges are pseudo-critical.

 

Constraints:

• 2 <= n <= 100
• 1 <= edges.length <= min(200, n * (n - 1) / 2)
• edges[i].length == 3
• 0 <= ai < bi < n
• 1 <= weighti <= 1000
• All pairs (ai, bi) are distinct.

Solution

---

Python3

class UnionFindSet:
    def __init__(self, n=0):
        self.parents = {}
        self.ranks = {}
        self.count = 0
        for i in range(n):
            self.add(i)
 
    def add(self, p):
        self.parents[p] = p
        self.ranks[p] = 1
        self.count += 1
 
    def find(self, u):
        if u != self.parents[u]:
            self.parents[u] = self.find(self.parents[u])
        return self.parents[u]
 
    def union(self, u, v):
        pu, pv = self.find(u), self.find(v)
        if pu == pv: 
            return False
        if self.ranks[pu] < self.ranks[pv]:
            self.parents[pu] = pv
        elif self.ranks[pu] > self.ranks[pv]:
            self.parents[pv] = pu
        else:        
            self.parents[pv] = pu
            self.ranks[pu] += 1
        self.count -= 1
        return True
    
# UnionFind + Kruskal + Enumerate edges
# O(ElogE + E^2 + E^2)
class Solution:
    def findCriticalAndPseudoCriticalEdges(self, n: int, edges: List[List[int]]) -> List[List[int]]:
        # sort edges in asc order based on weight
        edges = [(u, v, w, i) for i, (u, v, w) in enumerate(edges)]
        edges.sort(key=lambda x: x[2])
        
        # do not use this edge
        def find_mst_without_this_edge(edge_idx):
            union_find_set = UnionFindSet(n)
            ans = 0
            for i, (u, v, w, _) in enumerate(edges):
                # do not use this edge
                if i == edge_idx:
                    continue
                if union_find_set.union(u, v):
                    ans += w
            parent = union_find_set.find(0)
            return ans if all(union_find_set.find(i) == parent for i in range(n)) else inf
        
        # need to use this edge
        def find_mst_with_this_edge(edge_idx):
            union_find_set = UnionFindSet(n)
            # use this edge first
            u0, v0, w0, _ = edges[edge_idx]
            ans = w0
            union_find_set.union(u0, v0)
            for i, (u, v, w, _) in enumerate(edges):
                # do not use this edge
                if i == edge_idx:
                    continue
                if union_find_set.union(u, v):
                    ans += w
            parent = union_find_set.find(0)
            return ans if all(union_find_set.find(i) == parent for i in range(n)) else inf
        
        # normal MST total weight
        base = find_mst_without_this_edge(-1)
        cri, p_cri = set(), set()
        for i in range(len(edges)):
            wgt_excl = find_mst_without_this_edge(i)
            # if not included, MST total weight would increase
            if wgt_excl > base:
                cri.add(edges[i][3])
            else:
                wgt_incl = find_mst_with_this_edge(i)
                # with this edge, MST total weight doesn't change
                if wgt_incl == base:
                    p_cri.add(edges[i][3])
    
        return [cri, p_cri]