2316. Count Unreachable Pairs of Nodes in an Undirected Graph

Problem Link

Description

---

You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

Return the number of pairs of different nodes that are unreachable from each other.

 

Example 1:

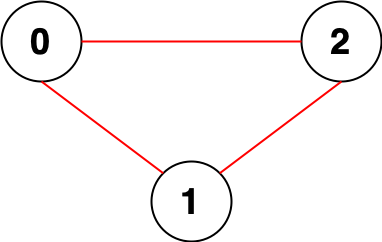
Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

Example 2:

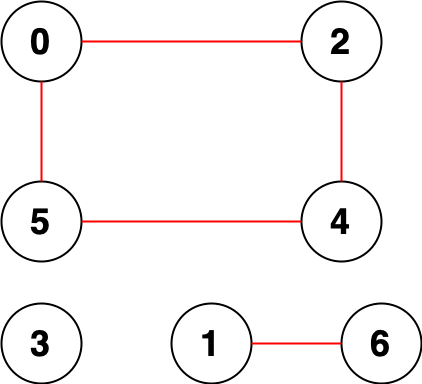
Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

 

Constraints:

• 1 <= n <= 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• There are no repeated edges.

Solution

---

Python3

class DSU:
    def __init__(self, n):
        self.parent = list(range(n))
        self.size = [1] * n
    
    def find(self, x):
        while x != self.parent[x]:
            self.parent[x] = self.parent[self.parent[x]]
            x = self.parent[x]
        
        return x
 
    def union(self, a, b):
        a, b = self.find(a), self.find(b)
        if a == b: return
 
        # to mainttain self.size[a] >= self.size[b]
        if self.size[a] < self.size[b]:
            a, b = b, a
        
        self.size[a] += self.size[b]
        self.parent[b] = a
 
class Solution:
    def countPairs(self, n: int, edges: List[List[int]]) -> int:
        uf = DSU(n)
 
        for a, b in edges:
            uf.union(a, b)
        
        parentCount = [0] * n
        parent = [-1] * n
 
        for i in range(n):
            p = uf.find(i)
            parentCount[p] += 1
            parent[i] = p
        
        res = 0
        for i in range(n):
            res += n - parentCount[parent[i]]
        
        return res // 2