3197. Find the Minimum Area to Cover All Ones II

Problem Link

Description

---

You are given a 2D binary array grid. You need to find 3 non-overlapping rectangles having non-zero areas with horizontal and vertical sides such that all the 1's in grid lie inside these rectangles.

Return the minimum possible sum of the area of these rectangles.

Note that the rectangles are allowed to touch.

 

Example 1:

Input: grid = [[1,0,1],[1,1,1]]

Output: 5

Explanation:

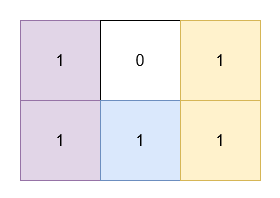
• The 1's at (0, 0) and (1, 0) are covered by a rectangle of area 2.
• The 1's at (0, 2) and (1, 2) are covered by a rectangle of area 2.
• The 1 at (1, 1) is covered by a rectangle of area 1.

Example 2:

Input: grid = [[1,0,1,0],[0,1,0,1]]

Output: 5

Explanation:

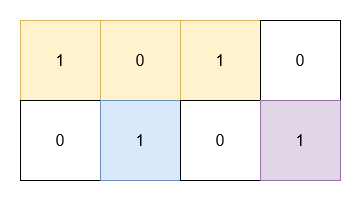
• The 1's at (0, 0) and (0, 2) are covered by a rectangle of area 3.
• The 1 at (1, 1) is covered by a rectangle of area 1.
• The 1 at (1, 3) is covered by a rectangle of area 1.

 

Constraints:

• 1 <= grid.length, grid[i].length <= 30
• grid[i][j] is either 0 or 1.
• The input is generated such that there are at least three 1's in grid.

Solution

---

Python3

class Solution:
    def minimumSum(self, grid: List[List[int]]) -> int:
        rows, cols = len(grid), len(grid[0])
 
        def count(r1, c1, r2, c2):
            minR, maxR = inf, -inf
            minC, maxC = inf, -inf
            
            for i in range(r1, r2 + 1):
                for j in range(c1, c2 + 1):
                    if grid[i][j] == 1:
                        minR = min(minR, i)
                        maxR = max(maxR, i)
                        minC = min(minC, j)
                        maxC = max(maxC, j)
            
            return (maxR - minR + 1) * (maxC - minC + 1)
        
        @cache 
        def go(r1, c1, r2, c2, splits):
            if splits == 1: return count(r1, c1, r2, c2)
 
            res = inf
 
            if splits == 2:
                for r in range(r1, r2):
                    res = min(res, go(r1, c1, r, c2, 1) + go(r + 1, c1, r2, c2, 1))
                
                for c in range(c1, c2):
                    res = min(res, go(r1, c1, r2, c, 1) + go(r1, c + 1, r2, c2, 1))
            elif splits == 3:
                for r in range(r1, r2):
                    res = min(res, go(r1, c1, r, c2, 1) + go(r + 1, c1, r2, c2, 2))
                    res = min(res, go(r1, c1, r, c2, 2) + go(r + 1, c1, r2, c2, 1))
                
                for c in range(c1, c2):
                    res = min(res, go(r1, c1, r2, c, 1) + go(r1, c + 1, r2, c2, 2))
                    res = min(res, go(r1, c1, r2, c, 2) + go(r1, c + 1, r2, c2, 1))
            
            return res
 
        
        return go(0, 0, rows - 1, cols - 1, 3)