3071. Minimum Operations to Write the Letter Y on a Grid

Problem Link

Description

---

You are given a 0-indexed n x n grid where n is odd, and grid[r][c] is 0, 1, or 2.

We say that a cell belongs to the Letter Y if it belongs to one of the following:

• The diagonal starting at the top-left cell and ending at the center cell of the grid.
• The diagonal starting at the top-right cell and ending at the center cell of the grid.
• The vertical line starting at the center cell and ending at the bottom border of the grid.

The Letter Y is written on the grid if and only if:

• All values at cells belonging to the Y are equal.
• All values at cells not belonging to the Y are equal.
• The values at cells belonging to the Y are different from the values at cells not belonging to the Y.

Return the minimum number of operations needed to write the letter Y on the grid given that in one operation you can change the value at any cell to 0, 1, or 2.

 

Example 1:

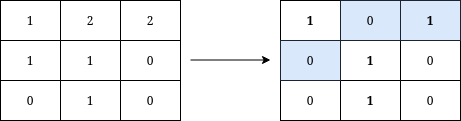
Input: grid = [[1,2,2],[1,1,0],[0,1,0]]
Output: 3
Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 1 while those that do not belong to Y are equal to 0.
It can be shown that 3 is the minimum number of operations needed to write Y on the grid.

Example 2:

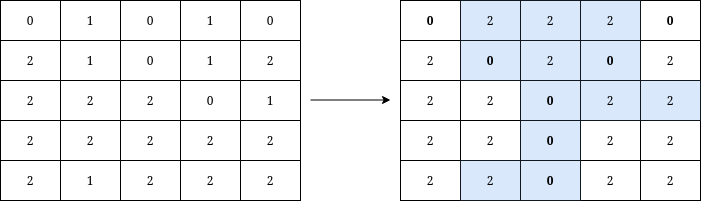
Input: grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]]
Output: 12
Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 0 while those that do not belong to Y are equal to 2. 
It can be shown that 12 is the minimum number of operations needed to write Y on the grid.

 

Constraints:

• 3 <= n <= 49
• n == grid.length == grid[i].length
• 0 <= grid[i][j] <= 2
• n is odd.

Solution

---

Python3

class Solution:
    def minimumOperationsToWriteY(self, grid: List[List[int]]) -> int:
        N = len(grid)
        total = [0, 0, 0]
        Y = [0, 0, 0]
        
        for i in range(N):
            for j in range(N):
                total[grid[i][j]] += 1
        
        cx = cy = N // 2
        
        x = y = 0
        while x != cx and y != cy:
            Y[grid[x][y]] += 1
            x += 1
            y += 1
 
        x, y = 0, N - 1
        while x != cx and y != cy:
            Y[grid[x][y]] += 1
            x += 1
            y -= 1
 
        for x in range(cx, N):
            Y[grid[x][cy]] += 1
        
        for i in range(3):
            total[i] -= Y[i]
        
        def go(a, b):
            # change Y to a
            res = sum(Y) - Y[a]
            
            # change total to b
            res += sum(total) - total[b]
            
            return res
            
        res = inf
        for a in [0, 1, 2]:
            for b in [0, 1, 2]:
                if a != b:
                    res = min(res, go(a, b))
        
        return res