3218. Minimum Cost for Cutting Cake I

Problem Link

Description

---

There is an m x n cake that needs to be cut into 1 x 1 pieces.

You are given integers m, n, and two arrays:

• horizontalCut of size m - 1, where horizontalCut[i] represents the cost to cut along the horizontal line i.
• verticalCut of size n - 1, where verticalCut[j] represents the cost to cut along the vertical line j.

In one operation, you can choose any piece of cake that is not yet a 1 x 1 square and perform one of the following cuts:

1. Cut along a horizontal line i at a cost of horizontalCut[i].
2. Cut along a vertical line j at a cost of verticalCut[j].

After the cut, the piece of cake is divided into two distinct pieces.

The cost of a cut depends only on the initial cost of the line and does not change.

Return the minimum total cost to cut the entire cake into 1 x 1 pieces.

 

Example 1:

Input: m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]

Output: 13

Explanation:

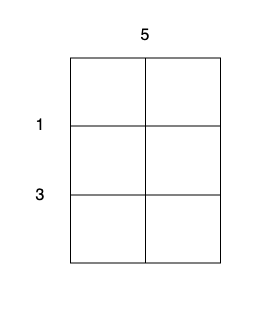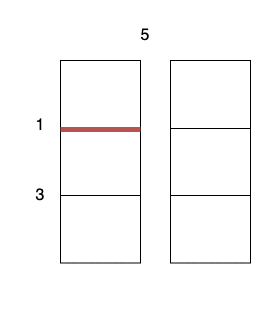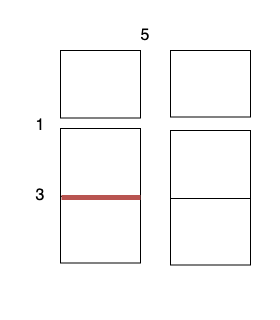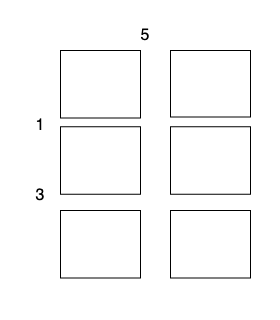
• Perform a cut on the vertical line 0 with cost 5, current total cost is 5.
• Perform a cut on the horizontal line 0 on 3 x 1 subgrid with cost 1.
• Perform a cut on the horizontal line 0 on 3 x 1 subgrid with cost 1.
• Perform a cut on the horizontal line 1 on 2 x 1 subgrid with cost 3.
• Perform a cut on the horizontal line 1 on 2 x 1 subgrid with cost 3.

The total cost is 5 + 1 + 1 + 3 + 3 = 13.

Example 2:

Input: m = 2, n = 2, horizontalCut = [7], verticalCut = [4]

Output: 15

Explanation:

• Perform a cut on the horizontal line 0 with cost 7.
• Perform a cut on the vertical line 0 on 1 x 2 subgrid with cost 4.
• Perform a cut on the vertical line 0 on 1 x 2 subgrid with cost 4.

The total cost is 7 + 4 + 4 = 15.

 

Constraints:

• 1 <= m, n <= 20
• horizontalCut.length == m - 1
• verticalCut.length == n - 1
• 1 <= horizontalCut[i], verticalCut[i] <= 103

Solution

---

Python3

class Solution:
    def minimumCost(self, m: int, n: int, horizontalCut: List[int], verticalCut: List[int]) -> int:
        
        @cache
        def go(x1, y1, x2, y2):
            if abs(x1 - x2) == 1 and abs(y1 - y2) == 1: return 0
            
            res = inf
            
            for y in range(y1 + 1, y2):
                c = verticalCut[y - 1]
                res = min(res, c + go(x1, y1, x2, y) + go(x1, y, x2, y2))
            
            for x in range(x1 + 1, x2):
                c = horizontalCut[x - 1]
                res = min(res, c + go(x1, y1, x, y2) + go(x, y1, x2, y2))
            
            return res
        
        return go(0, 0, m, n)