Description
You are given an array nums which is a permutation of [0, 1, 2, ..., n - 1]. The score of any permutation of [0, 1, 2, ..., n - 1] named perm is defined as:
score(perm) = |perm[0] - nums[perm[1]]| + |perm[1] - nums[perm[2]]| + ... + |perm[n - 1] - nums[perm[0]]|
Return the permutation perm which has the minimum possible score. If multiple permutations exist with this score, return the one that is lexicographically smallest among them.
Example 1:
Input: nums = [1,0,2]
Output: [0,1,2]
Explanation:
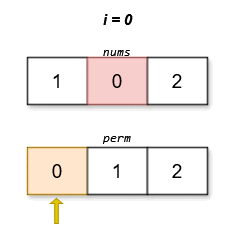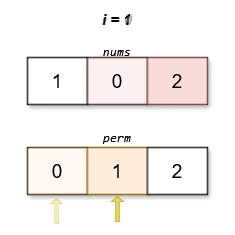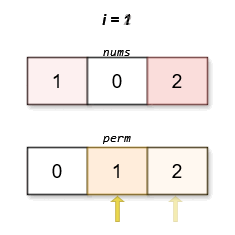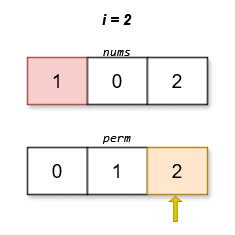
The lexicographically smallest permutation with minimum cost is [0,1,2]. The cost of this permutation is |0 - 0| + |1 - 2| + |2 - 1| = 2.
Example 2:
Input: nums = [0,2,1]
Output: [0,2,1]
Explanation:
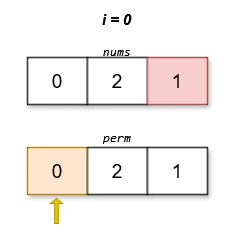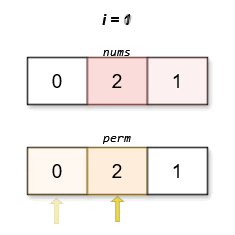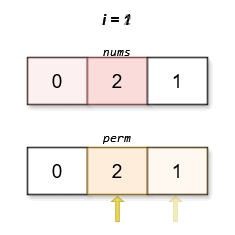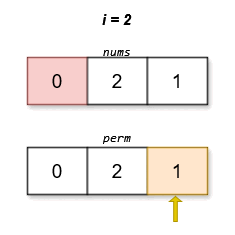
The lexicographically smallest permutation with minimum cost is [0,2,1]. The cost of this permutation is |0 - 1| + |2 - 2| + |1 - 0| = 2.
Constraints:
2 <= n == nums.length <= 14numsis a permutation of[0, 1, 2, ..., n - 1].
Solution
Python3
class Solution:
def findPermutation(self, nums: List[int]) -> List[int]:
N = len(nums)
full_mask = (1 << N) - 1
nxt = {}
# The score function is cyclic, so we can always set perm[0] = 0 for the smallest lexical order.
@cache
def go(mask, last):
if mask == full_mask:
nxt[(mask, last)] = (mask, last)
return abs(last - nums[0])
res = inf
for i in range(N):
if mask & (1 << i): continue
score = go(mask | (1 << i), i) + abs(last - nums[i])
if score < res:
res = score
nxt[(mask, last)] = (mask | (1 << i), i)
return res
go(1, 0)
res = []
curr = (1, 0)
for _ in range(N):
res.append(curr[1])
curr = nxt[curr]
return res