2711. Difference of Number of Distinct Values on Diagonals

Problem Link

Description

---

Given a 2D grid of size m x n, you should find the matrix answer of size m x n.

The cell answer[r][c] is calculated by looking at the diagonal values of the cell grid[r][c]:

• Let leftAbove[r][c] be the number of distinct values on the diagonal to the left and above the cell grid[r][c] not including the cell grid[r][c] itself.
• Let rightBelow[r][c] be the number of distinct values on the diagonal to the right and below the cell grid[r][c], not including the cell grid[r][c] itself.
• Then answer[r][c] = |leftAbove[r][c] - rightBelow[r][c]|.

A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until the end of the matrix is reached.

• For example, in the below diagram the diagonal is highlighted using the cell with indices (2, 3) colored gray:

  <ul>
  	<li>Red-colored cells are left and above the cell.</li>
  	<li>Blue-colored cells are right and below the cell.</li>
  </ul>
  </li>
  

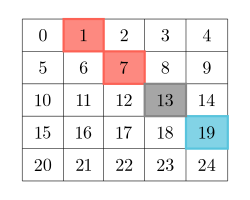
Return the matrix answer.

 

Example 1:

Input: grid = [[1,2,3],[3,1,5],[3,2,1]]

Output: Output: [[1,1,0],[1,0,1],[0,1,1]]

Explanation:

To calculate the answer cells:

answer	left-above elements	leftAbove	right-below elements	rightBelow	|leftAbove - rightBelow|
[0][0]	[]	0	[grid[1][1], grid[2][2]]	|{1, 1}| = 1	1
[0][1]	[]	0	[grid[1][2]]	|{5}| = 1	1
[0][2]	[]	0	[]	0	0
[1][0]	[]	0	[grid[2][1]]	|{2}| = 1	1
[1][1]	[grid[0][0]]	|{1}| = 1	[grid[2][2]]	|{1}| = 1	0
[1][2]	[grid[0][1]]	|{2}| = 1	[]	0	1
[2][0]	[]	0	[]	0	0
[2][1]	[grid[1][0]]	|{3}| = 1	[]	0	1
[2][2]	[grid[0][0], grid[1][1]]	|{1, 1}| = 1	[]	0	1

Example 2:

Input: grid = [[1]]

Output: Output: [[0]]

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n, grid[i][j] <= 50

Solution

---

Python3

class Solution:
    def differenceOfDistinctValues(self, grid: List[List[int]]) -> List[List[int]]:
        rows, cols = len(grid), len(grid[0])
        res = [[0] * cols for _ in range(rows)]
        
        for i in range(rows):
            for j in range(cols):
                topLeft, bottomRight = set(), set()
                
                a, b = i + 1, j + 1
                while a < rows and b < cols:
                    bottomRight.add(grid[a][b])
                    a += 1
                    b += 1
                
                a, b = i - 1, j - 1
                while a >= 0 and b >= 0:
                    topLeft.add(grid[a][b])
                    a -= 1
                    b -= 1
                
                res[i][j] = abs(len(topLeft) - len(bottomRight))
        
        return res