3240. Minimum Number of Flips to Make Binary Grid Palindromic II

Problem Link

Description

---

You are given an m x n binary matrix grid.

A row or column is considered palindromic if its values read the same forward and backward.

You can flip any number of cells in grid from 0 to 1, or from 1 to 0.

Return the minimum number of cells that need to be flipped to make all rows and columns palindromic, and the total number of 1's in grid divisible by 4.

 

Example 1:

Input: grid = [[1,0,0],[0,1,0],[0,0,1]]

Output: 3

Explanation:

Example 2:

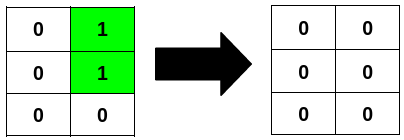
Input: grid = [[0,1],[0,1],[0,0]]

Output: 2

Explanation:

Example 3:

Input: grid = [[1],[1]]

Output: 2

Explanation:

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m * n <= 2 * 105
• 0 <= grid[i][j] <= 1

Solution

---

Python3

class Solution:
    def minFlips(self, grid: List[List[int]]) -> int:
        rows, cols = len(grid), len(grid[0])
        flips = totalOnes = symmetricPairs = 0
 
        for i in range((rows + 1) // 2):
            for j in range((cols + 1) // 2):
                A = {(i, j), (i, cols - 1 - j), (rows - 1 - i, j), (rows - 1 - i, cols - 1 - j)}
                count = len(A)
                ones = sum(grid[x][y] for x, y in A)
                zeroes = count - ones
                flips += min(ones, zeroes) # flip all ones -> zeroes or zeroes -> ones
                
                if ones == zeroes and count == 2:
                    symmetricPairs += 1
                
                if zeroes < ones: # means ideally will swap all zeroes to ones
                    totalOnes += count
 
        if totalOnes % 4 == 2 and symmetricPairs > 0:
            return flips
        
        if totalOnes % 4 == 3 and symmetricPairs > 0:
            return flips + 1
 
        return flips + (totalOnes % 4)