1462. Course Schedule IV

Problem Link

Description

---

There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course ai first if you want to take course bi.

• For example, the pair [0, 1] indicates that you have to take course 0 before you can take course 1.

Prerequisites can also be indirect. If course a is a prerequisite of course b, and course b is a prerequisite of course c, then course a is a prerequisite of course c.

You are also given an array queries where queries[j] = [uj, vj]. For the jth query, you should answer whether course uj is a prerequisite of course vj or not.

Return a boolean array answer, where answer[j] is the answer to the jth query.

 

Example 1:

Input: numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
Output: [false,true]
Explanation: The pair [1, 0] indicates that you have to take course 1 before you can take course 0.
Course 0 is not a prerequisite of course 1, but the opposite is true.

Example 2:

Input: numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
Output: [false,false]
Explanation: There are no prerequisites, and each course is independent.

Example 3:

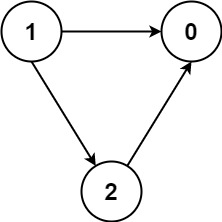
Input: numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
Output: [true,true]

 

Constraints:

• 2 <= numCourses <= 100
• 0 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)
• prerequisites[i].length == 2
• 0 <= ai, bi <= numCourses - 1
• ai != bi
• All the pairs [ai, bi] are unique.
• The prerequisites graph has no cycles.
• 1 <= queries.length <= 104
• 0 <= ui, vi <= numCourses - 1
• ui != vi

Solution

---

Python3

class Solution:
    def checkIfPrerequisite(self, N: int, prerequisites: List[List[int]], queries: List[List[int]]) -> List[bool]:
        indegree = [0] * N
        graph = defaultdict(list)
        queue = deque()
        prereq = defaultdict(set)
 
        for a, b in prerequisites:
            graph[a].append(b)
            indegree[b] += 1
 
        for node in range(N):
            if indegree[node] == 0:
                queue.append(node)
        
        while queue:
            node = queue.popleft()
 
            for adj in graph[node]:
                indegree[adj] -= 1
                prereq[adj].add(node)
                prereq[adj] |= prereq[node]
 
                if indegree[adj] == 0:
                    queue.append(adj)
        
        res = []
        for a, b in queries:
            res.append(a in prereq[b])
 
        return res